Kreispackung in einem Kreis

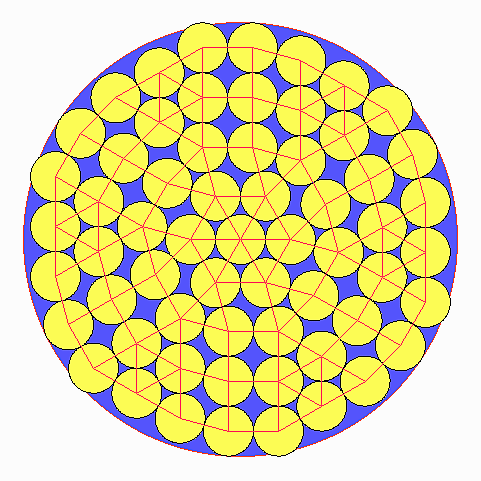
Die Kreispackung in einem Kreis ist ein zweidimensionales Packungsproblem der Mathematik. Es beschäftigt sich mit der Frage, wie viele Kreise gleicher Größe in einen größeren Kreis hineinpassen.

Problem

Unter einer Kreispackung in einem Kreis versteht man die überlappungsfreie Anordnung einer vorgegebenen Zahl von Kreisen mit gleichem Radius innerhalb eines größeren Kreises. Für das Packungsproblem gibt es zwei gleichwertige Fragestellungen:

1. Wie groß dürfen die kleineren Kreise sein, damit ${\displaystyle n}$ Stück von ihnen in einen großen Kreis mit gegebenem Radius passen?
2. Welchen Radius muss der große Kreis mindestens haben, damit ${\displaystyle n}$ Einheitskreise hineinpassen?

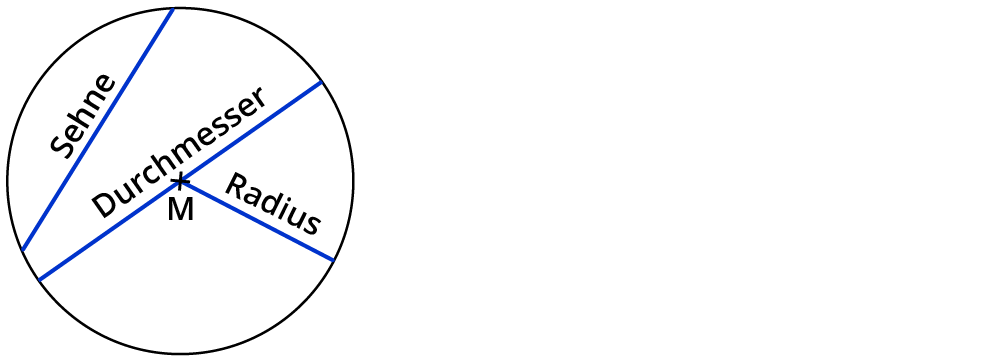
Bei beiden Fragen kommt es nur auf das Verhältnis der beiden Radien an. Bezeichnet ${\displaystyle R}$ den Radius des großen Kreises und ${\displaystyle r}$ den Radius der kleinen Kreise, dann ist die Packungsdichte ${\displaystyle P}$ der Kreispackung durch

${\displaystyle P={\frac {n\cdot r^{2}}{R^{2}}}}$

gegeben.

Geschichte

Dieses Packungsproblem wurde zuerst in den 1960er Jahren gestellt und untersucht. Sidney Kravitz veröffentlichte im Jahr 1967 Packungen mit bis zu 19 Kreisen, ohne die Optimalität der Lösungen zu betrachten. Ein Jahr später bewies Graham, dass die gefundenen Anordnungen mit höchstens 7 Kreisen optimal sind, und von ihm unabhängig Pirl, dass die Anordnungen mit höchstens 10 Kreisen optimal sind. Erst 1994 wurde die Optimalität der Lösung mit 11 Kreisen von Hans Melissen bewiesen. Ferenc Fodor zeigte zwischen 1999 und 2003, dass die Lösungen mit 12, 13 und 19 Kreisen optimal sind.

Darüber hinaus sind nur Näherungslösungen bekannt. Graham et al. etwa gaben 1998 zwei Algorithmen und die damit gefundenen Packungen mit bis zu 65 Kreisen an. Eine Übersicht und Näherungslösungen mit bis zu 2989 Kreisen stammt von Eckard Specht.

Übersicht über die ersten 20 Fälle

Diese Tabelle gibt an, wie klein man den Außenkreis machen kann, wenn er eine vorgegebene Anzahl an Einheitskreisen enthalten soll. In einigen Fällen gibt es mehr als eine Anordnung.

Wenn die äußeren Kreise einen geschlossenen „Ring“ bilden wie in den Fällen n = 3, 4, 5, 6, 7, 8, 9, 11, 13, 18, 19, dann ergibt sich das Verhältnis der Radien als

${\displaystyle {\frac {R}{r}}=1 {\frac {1}{\sin {\tfrac {\pi }{k}}}}}$

wobei ${\displaystyle k}$ die Anzahl der Kreise in diesem „Ring“ ist. Der Bruch entspricht dabei dem Umkreisradius eines regelmäßigen Polygons mit ${\displaystyle k}$ Ecken und Seitenlänge ${\displaystyle 2}$.

Für 12 Kreise zum Beispiel ergibt sich das Verhältnis der Radien implizit als

${\displaystyle {\frac {R}{r}}=1 {\frac {2}{{\sqrt {3}}\cdot x_{0}}}}$

wobei ${\displaystyle x_{0}}$ die kleinste Nullstelle des Polynoms ${\displaystyle 9\cdot x^{5}-15\cdot x^{4} 7\cdot x^{3}-3\cdot x 1=0}$ ist.

Dichteste Kreispackung in der zweidimensionalen Ebene

In der zweidimensionalen Ebene ohne äußeren Kreis hat die dichteste Kreispackung die Packungsdichte

${\displaystyle P={\frac {\pi \cdot {\sqrt {3}}}{6}}\approx 0{,}907}$

Entscheidende Beiträge dazu lieferten Joseph Louis Lagrange im Jahr 1773 und Axel Thue im Jahr 1890. Der allgemeine Fall ohne Gitterstruktur wurde im Jahr 1942 von László Fejes Tóth bewiesen.

Zusammenhang mit der Kreispackung in einem Kreis

Ist ${\displaystyle P_{n}}$ die Packungsdichte für die dichteste Kreispackung von ${\displaystyle n}$ gleich großen Kreisen in einem Kreis, dann gilt für den Grenzwert

${\displaystyle \lim _{n\to \infty }P-P_{n}=\lim _{n\to \infty }{\frac {\pi \cdot {\sqrt {3}}}{6}}-P_{n}=0}$

Die Packungsdichte ${\displaystyle P_{n}}$ nähert sich also für große ${\displaystyle n}$ immer mehr der Packungsdichte ${\displaystyle P}$ ohne äußeren Kreis an.

Verallgemeinerung

Die dreidimensionale Verallgemeinerung des Packungsproblems ist die dichteste Kugelpackung in einer Kugel. Auch im dreidimensionalen Fall sind einige optimale Anordnungen bekannt.

Siehe auch

• Apollonios-Kreisfüllung

Literatur

• Packing equal circles into squares, circles, spheres. In: János Pach, Peter Brass, W. O. J. Moser: Research problems in discrete geometry, Springer Verlag 2005, S. 28–43, bes. S. 30.

Weblinks

• Eric W. Weisstein: Circle Packing. In: MathWorld (englisch).
• Eckard Specht: The best known packings of equal circles in a circle (complete up to N = 2600). packomania.com, letzte Aktualisierung: 10. Juni 2014
• Erich Friedman: Circles in Circles

Einzelnachweise